Objetivos
Discutir alguns aspectos sobre as representações de números complexos e suas propriedades; particularmente, estudar exponenciais complexas.
Definição
Um número complexo z é definido como sendo o par (a,b), em que a e b são números reais,
sujeito às seguintes regras algébricas:
dados e
- Igualdade –
- Adição e Subtração –
- Multiplicação –
- Divisão –
As operações acima possuem as mesmas propriedades das respectivas operações definidas para os números reais (comutatividade, associatividade e distributividade), definindo-se:
- Elemento neutro da adição –
- Elemento neutro da multiplicação –
Adicionalmente, define-se a chamada unidade imaginária como sendo
A unidade imaginária tem as seguintes propriedades operatórias:
- propriedade 1 –
- propriedade 2 –
O número z = (a,b) assim definido é denominado de complexo, por ser formado por mais de uma componente numérica, sendo suas componentes a e b denominadas respecivamente de parte real e parte imaginária e escreve-se
eee
.
Número complexo conjugado
Define-se o conjugado do número complexo z = (a,b) como sendo o número .
- propriedade do conjugado –
A grandeza |z| denomina-se o módulo do número complexo z.
.
Representação Geométrica
.
Coordenadas cartesianas
O número complexo z = (a,b) é representado em coordenadas cartesianas por z = a + i b .
A figura 1 apresenta uma representação gráfica de z. O sistema de coordenadas cartesianas representa a parte real no eixo das abcissas e a parte imaginária
no eixo das ordenadas.

Figura 1 – Representação geométrica de um número complexo
O número complexo é representado graficamente como o vetor de coordenadas . Os versores dos eixos coordenados são, respectivamente (1,0) para o eixo real e (0,1) para o eixo imaginário. Neste caso (0,1) é interpretado como a unidade imaginária também. O plano cartesiano assim construído é denominado de plano complexo ou plano de Argand – Gauss.
Potências de i
Na notação cartesiana, temos:
e assim por diante. Definindo-se e considerando-se os resultados acima, observa-se repetição periódica do padrão
na forma de uma série tal que
A tabela abaixo exibe alguns exemplos de valores dessa série.
.
Tabela 1 – Potências da unidade imaginária
.
Coordenadas Polares
O número complexo z = a + i b na forma cartesiana, pode também ser representado na forma polar, dada por . A coordenada
é dita o módulo de z e a coordenada
é dita argumento ou fase de z.
Valem as seguintes relações:
- transformação cartesiana -> polar:
- transformação polar -> cartesiana:
A igualdade entre dois números complexos pode agora ser escrita como:
Dados e
tem-se
.
As operações de multiplicação, divisão, potenciação e radiciação são expressas de maneira mais simples em coordenadas polares:
dados e
- Multiplicação –
- Divisão –
- Potenciação –
- Radiciação –
A operação de adição de dois números complexos é representada graficamente pela adição vetorial dos dois vetores representativos dos números complexos somados, conforme mostrado na figura 2.

Figura 2 – Adição e subtração dos números complexos z1 e z2
A multiplicação e a divisão também podem ser apresentadas como operações gráficas entre vetores (segmentos orientados) no plano complexo. Entretanto, são construções de interesse mais específico e as deixaremos de lado neste momento. Vamos apresentar dois casos particulares dessas construções, que são a multiplicação e divisão pela unidade imaginária .

Figura 3 – Multiplicação e divisão pela unidade imaginária
A divisão pela unidade imaginária também pode ser entendida como multiplicação por , uma vez que
Note-se, conforme ilustrado na figura 3, que multiplicar um número complexo por i equivale a girar esse número de 90 graus, sem alterar seu módulo. Da mesma forma, multiplicar z por -i equivale a girar z de -90 graus.
.
Fórmulas e notação de Euler
Os números complexos podem ainda ser apresentados em uma outra forma bastante útil, decorrente da fórmula de Euler. Se expandirmos a função exponencial em série de Mac Laurin (ou série de Taylor na origem) e fizermos a substituição
, obteremos:
Podemos reagrupar os termos dessa série da seguinte forma:
Nessa decomposição consideramos as potências de i , tal como mostradas na tabela 1 acima. Resulta, então:
Podemos identificar o primeiro somatório como sendo a expansão em série de Mac Laurin do e o segundo somatório como sendo a expansão em série de Mac Laurin do
.
O resultado assim obtido denomina-se fórmula de Euler, expressa como:
Pode-se utlizar essa expressão para demonstrar as seguintes relações de Euler:
Essas expressões podem ser também verificadas graficamente, no plano de Argand, como ilustrado na figura4 a seguir. Na figura 4, chamamos , sendo o seu conjugado
, portanto. Verifica-se graficamente, na fig.4, que
…… e …..
… , …demonstrando, assim, as relações de Euler.

Figura 4 – Relações de Euler para o co-seno e o seno
Note que, no plano de Argand os vetores alinhados de modo estritamente vertical são escritos como .
.
Raízes da unidade
A potenciação no corpo complexo pode ser deduzida utilizando-se a definição da multiplicação em coordenadas polares e aplicando-se a mesma diversas vezes, provando-se por indução finita o resultado já apresentado : .
Particularizando para o caso em que z = 1,
obtem-se a chamada fórmula de Moivre:
Para obter-se a expressão da radiciação deve-se resolver , ou seja, considerando-se
e
, tem-se:
e, portanto
Dois números complexos são iguais se forem iguais seus módulos e suas fases, respectivamente. Logo:
.
e, consequentemente, .
No caso das raízes da unidade, tem-se: e, portanto:
Portanto, extraindo-se a raiz n-ésima, obtem-se n raizes da unidade. Usualmente denota-se por a raiz para k=1. Empregando-se a fórmula de Moivre, conclui-se que para um k genérico,
a raiz pode ser escrita em termos de w como
.
Isto é, as raízes serão
,
sendo .
No plano de Argand, as raízes n-ésimas da unidade distribuem-se sobre o círculo initério (centrado na origem), correspondendo aos vértices de um polígono regular de n lados inscrito no círculo, conforme ilustrado na figura 5 abaixo.

Figura 5 – Raízes da unidade, para n=4 e n=6, respectivamente.

45 comentários
Comments feed for this article
junho 23, 2008 às 8:27 pm
Série de Fourier e Transformada de Fourier - I « Videlicet
[…] As funções sin(x) e cos(x) podem ser apresentadas como (ver post anterior) […]
outubro 1, 2008 às 1:13 pm
Luiz
como faço para achar o módulo de z=3 elevado a 1/4?
outubro 5, 2008 às 2:37 pm
Joao Kogler
Luiz,
note que o módulo de um número complexo é um número real, o que simplifica bastante o cálculo. Além disso, lembre que elevar a uma potência fracionária envolve extrair a raiz da ordem igual ao valor do denominador do expoente. Ou seja, o que você deseja pode traduzir-se por extrair a raiz quarta de 3, isto é:
novembro 11, 2008 às 6:39 pm
Pedro
Obrigado pela ajuda !!
novembro 22, 2008 às 6:40 pm
Castanheira
Obrigado, realmente dá muito jeito este site, encontrei por acaso mas recomendo…Dá jeito para Engenharia Electrotecnica
novembro 24, 2008 às 1:45 am
Leonardo
Bom, queria saber porex se houver uma questao fazendo
(a + ib)^6
como faria?
orbigado
novembro 28, 2008 às 12:47 am
Joao Kogler
Leonardo, converta o número a + ib para a forma polar e então calcule a potência.
dezembro 1, 2008 às 7:13 pm
luciano
O módolo do número complexo(1+3i)a tercera é?
dezembro 5, 2008 às 12:01 pm
Joao Kogler
Luciano, veja no post como calcular a potência de um número complexo. Ele tem de estar antes de tudo na forma polar. O módulo ao cubo surgirá naturalmente no processo.
março 15, 2009 às 2:24 am
Pedro
Caro professor Kogler, espero não abusar da sua boa vontade, mas eu gostaria de perguntar ao senhor qual é o resultado que dá se elevarmos o numero i (raiz de -1) a i (raiz de -1)? Vi essa questão em um desafio de uma aula e tentei fazer. Eu cheguei em e elevado a pi/2. Tá certo?
março 15, 2009 às 2:24 am
Pedro
ops, e elevado a menos pi/2
março 15, 2009 às 2:49 am
Joao Kogler
Pedro, está correto, pois
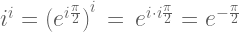
março 18, 2009 às 3:02 pm
Claudinei
Kloger: Encontrei o que acho que são alguns erros de edição nas fórmulas apresentadas:
Na adição e subtração o certo é:
Na multiplicação o certo é: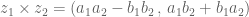
Finalmente, no quadrado de i: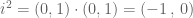
ou simplesmente -1.
Por favor, verifique e acerte, se for o caso.
Obrigado
Claudinei
março 30, 2009 às 12:34 am
Joao Kogler
Claudinei, obrigado pela revisão. As correções foram feitas.
julho 15, 2009 às 12:17 am
raniere elias tavares
gostaria de obter um video sobre a historia dos numeros complexos e se posivel um video da aplicação destes numeros na fisica e/ou geometria fractal eou outras aplicaçoes
julho 15, 2009 às 2:54 pm
Joao Kogler
Não tenho informações sobre videos a esses respeitos.
Talvez encontre algo no YouTube.
Veja alguns exemplos em:
http://www.youtube.com/view_play_list?p=33EF042C96815B41
Entretanto, há alguns livros recomendáveis:
Paul Nahin
An Imaginary Tale: The Story of “i” [the square root of minus one]
Tristan Needham
Visual Complex Analysis
Robert Devaney
Chaos,Fractals and Dynamics – Computer experiments in mathematics
abril 3, 2010 às 6:29 pm
adilson
como é k faço para axar o resultado de Z=(1/2+a raiz de 3/2)
abril 3, 2010 às 6:32 pm
adilson
elevado a 100
julho 28, 2010 às 3:23 pm
dorothy_dora
Gostaria de saber tudo sobre propriedades exponenciais e logarítimicas
julho 25, 2011 às 6:25 pm
magna
qual é a forma complexa do cos ao quadrado?
agosto 14, 2011 às 2:10 pm
Joao Kogler
Há duas maneiras para você descobrir: 1.Escreva a forma complexa de cos(x) e eleve-a ao quadrado; 2. Use uma transformação trigonometrica para [cos(x)]^2 obtendo uma expressão em cos(2x) e ache a forma complexa desta expressão.
fevereiro 5, 2014 às 2:34 pm
Joel Rodrigues
Bom dia, como faço para somar ou diminuir duas coordenadas polares?
fevereiro 6, 2014 às 4:20 pm
Joao Kogler
Sua questão, colocada de forma mais precisa no contexto de números complexos seria “como se faz para somar ou subtrair números complexos representados em coordenadas polares”. O mais prático é transformar a representação para fora retangular, efetuar a adição ou subtração e transformar o resultado para a representação polar. Calculadoras e computadores fazem essas transformações de modo expedito. A alternativa é fazer seu próprio algoritmo, embutindo as transformações na expressão da operação, o que desaconselho.
março 26, 2014 às 4:13 pm
Geraldo Celso Ferreira Filho
Como descrever o conjunto de pontos az +b quando z varia no primeiro quadrante
abril 9, 2014 às 12:04 am
Rithie
Republicou isso em Zero Daye comentado:
ótimo post sobre números complexos e Fourrier.
maio 23, 2014 às 12:45 pm
Geraldo Celso Ferreira Filho
como determinar o valor de (1 + i) elevado a i
maio 23, 2014 às 12:46 pm
Geraldo Celso Ferreira Filho
determinar o valor de (1 +i) ^i
outubro 1, 2014 às 1:23 pm
nie
A raiz enésima de 1 é sempre 1. Há um erro no texto.
fevereiro 22, 2015 às 3:31 pm
Joao Kogler
http://en.wikipedia.org/wiki/Root_of_unity
janeiro 16, 2015 às 5:43 am
debora caldas
Professor, gostaria de saber o que devo fazer quando a parte imaginaria (i) acompanhar o cosseno. Eu derivei isen (kx -wt) em relaçao a t e o i passou a acompanhar o cosseno.
janeiro 16, 2015 às 4:22 pm
Joao Kogler
A unidade imaginária “i” é uma constante. Portanto. acompanhará multiplicando a derivada, que é cosseno. Está correto o que você fez.
janeiro 23, 2015 às 2:20 am
Diego
Não entendi porque a unidade imaginária “i” é uma constante, pode me ajudar
fevereiro 22, 2015 às 3:21 pm
Joao Kogler
março 18, 2015 às 3:22 pm
Vinícius
Veeeelho, eu me matando pra fazer essa questão de exponencial, sendo que era apenas uma noação, ou seja, outra forma de escrever a mesma coisa! kkkkkkkk, salvou minha vida rapaz! Eternas bençãos sobre ti!
março 28, 2015 às 12:16 am
Frederico Guizini Santos
Agradeço pelas informações que você colocou neste site e que me permitiram entender a equivalência da exponencial e^(i.teta)=cos (teta)+i.sin (teta) através da fórmula de Euler, aplicado ao meu estudo de soluções de equações diferenciais homogêneas a coeficientes constantes, com raízes complexas.
abril 24, 2016 às 1:20 pm
Daniela Lemes
Gostaria de saber como faço para encontrar o módulo ao quadrado de z da expressão z = (10-i).i^3 + i^50 / [(i-1)^2] Obrigada!
outubro 31, 2016 às 12:50 pm
Joao Kogler
Use a definição de módulo e eleve ao quadrado.
outubro 5, 2016 às 1:55 pm
José Arujo
Como calular Z^z na forma (a+bi)^(c+di)
Por exemlo (2+3 i)^(3+2i)
outubro 31, 2016 às 12:49 pm
Joao Kogler
Faça via manipulações algébricas, é o caminho. Aplique a definição de potência complexa que conhece na forma polar e manipule o resultado para chegar na forma retangular correspondente.
outubro 27, 2016 às 8:05 pm
Jassilena Pio Delgado
como demostrar que cos x=1 em numeros complexo
outubro 31, 2016 às 12:42 pm
Joao Kogler
cos(x) = 1 para qual valor de x ?
O cosseno é uma função que toma valores em [-1,1].
A parte real de um número complexo pode ser obtida através da projeção sobre o eixo real, para o que a função cos(argumento) é usada. De fato, não seria uma demonstração, mas um cálculo.
janeiro 13, 2017 às 8:21 pm
Gil Cleber
Bastante detalhado, mas eu senti falta de uma explicação acerca de como se calculam potências e raízes complexas: x^(a+bi) e x^(1/(a+bi)).
maio 14, 2017 às 8:16 pm
lucas
Como determinar o modulo de (1/10)e^(-jk(2pi/5))(sen(kpi/2)/sen(kpi/10)) ? Eu sei que o modulo de e^(-jk2pi/5) resulta em 1, mas não compreendo como encontrar o modulo de toda a expressão.
junho 27, 2017 às 3:32 am
Tilah
Quanto seria raiz de i elevado à quarta potência? Tipo: (sqrt (i))^4 .Seria igual a 1 ou -1? Chego nas duas respostas, não sei qual é a correta.
abril 5, 2020 às 7:33 pm
Daniel
Boa noite professor como determinar 𝐼=(4−𝑗3)𝐴 𝑜𝑢 𝐼=4−𝑗3,𝐴 na forma exponencial